第3章

数据类型

《C和指针》^[14]一书提到，C语言中仅有四种数据类型，分别为整型、浮点型、指针型和聚合类型（包含数组和结构体），剩下的类型都是从这四种类型派生或组合而来的。

例如字符型char其实就是一个短整型，而字符串是用字符数组来保存和模拟的。本章我们主要说说整型和浮点型的相关问题。字符串、指针、数组和结构等主题，我将在本书的后面章节介绍。整型家族还分为有符号（signed）和无符号（unsigned）两种。整型数无论是否有符号，在计算机内部都是用补码来表示的。理解补码的表示方式有助于我们对整型数溢出的理解，所以先来介绍整型数的补码表示。

3.1  原码、反码和补码的解释

介绍补码之前，先简单介绍一下计算机内部使用的二进制。人类用十进制完全是因为我们有10个手指头。如果有一天你看到一个外星人，它只有4个手指头，那么他使用的一定是四进制，如图3-1所示。

如果能看明白图3-1，说明你已经明白了进制和手指头的关系了。现代的计算机内部使用门电路，它们只能表示0或者1两个状态。如果计算机是一个人，那么他只有两个手指头，所以它使用二进制。所谓的进制，根本就不是什么神秘的东西。

图3-1  进制和手指头的关系

理解了计算机内部使用的二进制，下面来看看原码、反码和补码的官方定义。

·   原码：原码是一种计算机中对数字的二进制表示方法，数码序列中最高位为符号位，符号位为0表示正数，符号位为１表示负数；其余有效值部分用二进制的绝对值表示。

·   反码：如果机器数是正数，则该机器数的反码与原码一样；如果机器数是负数，则该机器数的反码是对它的原码（符号位除外）各位取反而得到的。

·   补码：如果机器数是正数，则该机器数的补码与原码一样；如果机器数是负数，则该机器数的补码是对它的原码（除符号位外）各位取反，并在末位加1。

这样的定义绝对正确，但是绝对也会让你一头雾水，其实我们可以通过画几个图把这些概念简单地阐述清楚。为了方便说明问题，我假定用4位二进制数表示一个整数[①]。

图3-2说明了无符号数的原码表示方法。其中内圈的数字为二进制数，外圈的数字为内圈二进制数所对应的十进制数[②]。

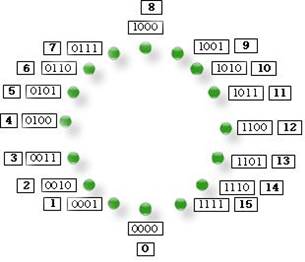
图3-2  无符号数的原码

顾名思义，无符号数不能表示负数。为了解决这个问题，我们把最高位定义为符号位。如果最高位为1就代表是一个负数，其他三位表示对应的十进制数。如图3-3所示，这就是有符号数的原码表示。

图3-3  有符号数的原码表示

用原码来表示一个有符号数会带来两个问题。第一个问题就是正负相加不等于零。如图3-3所示，1+(−1)，就是0001+1001=1010，按照原码表示等于−2。第二个问题就是有两个零存在，分别为0000和1000。可见，原码不适合用来表示有符号数！

为了保证正负相加等于零，我们采用了反码的表示方法，反码的表示如图3-4所示。如果把二进制数1000想象成12点，把二进制数0000想象成6点，原码就是从12点开始顺时针排列−1到−7，而反码就是从6点开始逆时针排列−1到−7。这样做的好处就在于现在正负数相加等于零了。例如1+(−1)，就是0001+1110=1111，用反码表示的话就是（−0）了。

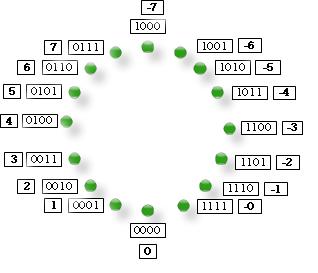
图3-4  有符号数的反码表示

第一个问题解决了，但是第二个问题还是没有解决，在用反码表示有符号数的图3-4中，依然有两个零存在，分别为0000和1111。聪明的读者一定已经猜到了，补码就是为了解决这个问题而发明的。

按照补码的定义，−1的反码为1110，不过现在必须在末位加1，那现在−1就是1111了。以此类推，补码的表示如图3-5。与反码表示不一样的是，补码在负数上从−1表示到−8，−0不再存在了。

图3-5  有符号数的补码表示

虽然第二个问题解决了，但用补码表示时，正负相加还等于零吗？我们可以自己验证一下，如果丢弃最高位的进位，结果满足正负相加等于零。至此，我们找到了终极的解决方案，那就是利用补码来表示一个有符号的整数。注意一点，对于无符号数，原码、反码、补码都是一致的。所以我们得到的最后结论是：整型数在计算机中，使用补码表示。

3.2  整型数的溢出

如果3.1节你已经完全明白了，那么下面我们开始讨论在实际编写程序中非常危险的一个bug，那就是C语言的整型数溢出问题。大家不要害怕，有了3.1节的基础，下面讨论的溢出问题会比较容易理解。

首先，我们知道，有符号数在计算机内部都是通过补码来表示的。其次，在图3-5中，如果加上x，就代表着顺时针走x格；如果减去x，就代表着逆时针走x格。有了这些知识，让我们用实例说话。在图3-5中，如果3+1，那就是从3顺时针走一格，等于4，没有任何问题。但是如果是7+1呢？顺时针走1格后，变成了−8了。如果7+7呢，顺时针走7格，等于−2了。这就是整型数发生了溢出。所谓的溢出，就是因为4位二进制数，用补码表示一个整数的时候，所能表示的最大正整数就是，如果在7的基础上再加1，就会发生“轻微溢出”，变为了最小的那个负数，如果两个最大的正整数相加，就会发生“严重溢出”。结果等于−2。这里注意，所谓的“轻微溢出”和“严重溢出”都是从溢出的角度去定义的。事实上，它们都是非常严重的bug，在实际编程中并不是说“严重溢出”就比“轻微溢出”更严重。

那么，C语言中int所表示的“最大正整数”到底是多少呢？不同的平台，不同的编译器，会有不同的定义。为此，C语言在头文件limits.h中给出了相关的宏定义，如表3-1所示。

表3-1  整型数的极限值宏定义

char	int	short	long	long long
SCHAR_MAX	INT_MAX	SHRT_MAX	LONG_MAX	LLONG_MAX
SCHAR_MIN	INT_MIN	SHRT_MIN	LONG_MIN	LLONG_MIN
UCHAR_MAX	UINT_MAX	USHRT_MAX	ULONG_MAX	ULLONG_MAX
CHAR_MIN
CHAR_MAX

有了这些宏定义，我们就可以编写出程序3-1，程序中分别演示了加法带来的溢出和减法带来的溢出。

程序3-1  溢出的实例

 

程序最后的运行结果如图3-6所示，最大的正整数为2⁽³²⁻¹⁾−1=2147483647。其他的数这里不解释了，读者可以按照反码的原理，自己解释并验证一下。

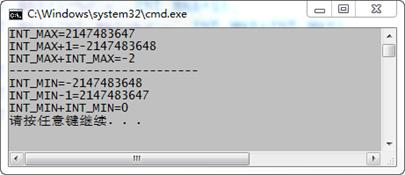
图3-6  程序运行结果

3.3  溢出深入分析

通过3.2节，我们已经初步知道了造成溢出的主要原因，但是只知道原因是不够的。下面我们对溢出的现象进行深入分析。本节主要说明4个子问题：溢出的定义，溢出发生的边界，溢出的危害以及如何避免溢出。

3.3.1  溢出的定义

关于有符号整型数的溢出，程序3-1已经阐述得很清楚了，大家对这个问题也没有什么异议。但是对于无符号数，《C陷阱与缺陷》^[2] 在“整数溢出”一节中指出，在无符号算术运算中，没有所谓的“溢出”一说。我想Koenig的思路可能是这样，当下午1点的时候，没有任何人会说：“现在是12点溢出了。”因为我们丫Ｊ缎缘刂溃颐堑闹颖砩鲜敲挥�13这个数字的。但是在C语言中，你能常识性地马上告诉我UINT_MAX是多少吗？下面我们看程序3-2。程序3-2中a是一个无符号整型数，运行这个程序后，会打印出“0”。

程序3-2  无符号整型数溢出的例子

假设现在你每个月赚UINT_MAX，由于你的工作出色，老板决定下个月给你涨一块钱。根据这段程序，你下个月工资将会是0元。这个时候，如果老板说无符号算术运算中没有“溢出”的话，你会同意吗？所以我决定不再讨论“溢出”是否有符号，而是从工程的角度来看，如果经过程序运算和经过纸和笔运算的结果不一样，那么我们就认为整型数运算发生了溢出。除了运算的溢出，C语言中还有很多其他类型的溢出，读者可以参考本书网站上“扩展内容”网页中的“谈谈C语言的溢出”。

3.3.2  溢出的边界

图3-7和图3-8分别演示了有符号数和无符号数中的两种溢出，分别为上溢出和下溢出。上溢出是由于顺时针方向旋转（加法）造成的。下溢出是由于逆时针方向旋转（减法）造成的。对于无符号数，溢出发生的地方在6点钟方向，如图3-7所示，而对于有符号数，溢出的边界在12点方向，如图3-8所示。

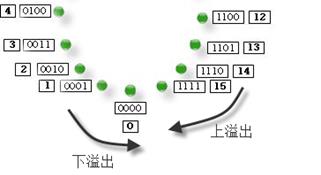
图3-7  无符号数的溢出边界

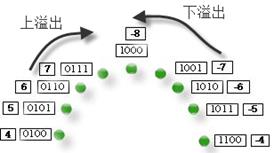
图3-8  有符号数的溢出边界

3.3.3  溢出的危害

溢出最令人沮丧的地方就在于，C语言不通过运行时检查来避免溢出[③]，所以程序3-2会正常地运行，没有任何提示和运行错误，你的工资莫名其妙地就变为零了。

当我学习C语言这门课的时候，邻座一美女同学，偷偷递给我一张纸条，纸条上写着程序3-3。我看了一眼对她说：“你没有考虑溢出啊！如果love溢出，会变成一个最小的负数。”然后我就把这个字条还给了那位美女同学。从此以后，她就再也没有联系过我。直到现在，我依然后悔，后悔只是关注了love的溢出，而没有关注time的溢出。

程序3-3  程序员的求爱信

 

溢出的危害如此严重，它能让你从亿万富翁一下变为穷光蛋，也能让你错失到手的爱情，还有什么比这更严重的呢？那为什么C语言不去避免这种错误呢？这符合C语言的两个风格：信任程序员，只要快。因为C语言信任你，所以编译器认为你写出UINT_MAX+1是对的，就算你把铅笔插到自己的鼻孔里，编译器也是认为你是对的，没有运行时检查是为了保证速度。假如你出门旅游的时候带着妈妈，我敢说这一路你是安全的，但是你一定快不起来。C语言就是这样，把妈妈放到家里，把铅笔插到鼻孔里，走你！

3.3.4  避免溢出的方法

聪明的读者一定都看出来了，上面关于美女和纸条的故事是杜撰的。实际的情况是我根本就没上过C语言的课，完全是自学成才。学成后写了一个十万行的程序，送给我暗恋的女孩，她看后十分感动，然后拒绝了我。实际编写工程的时候，溢出发生的概率和美女给你递纸条的概率一样，都不是很高，所以你也不用过分担心这个问题。避免溢出的一个最根本原则就是了解你要处理问题的规模，如果要处理一个班的学生，你完全可以忽略溢出问题；但是如果要处理全世界的人口，那么你就应该提高警惕了。

一个比较简单的避免溢出的方法就是利用double数据类型。一般情况下，让double溢出还真是件比较困难的事。如果要求一定要用整型数来完成任务，那么你首先应该利用表3-1中的宏定义，了解一下C语言在你所用平台上的极限值，并且利用这些宏定义和程序3-4中列出的判断表达式来避免溢出的发生。请注意，程序3-4中的判断表达式有的时候代表溢出会发生，有的时候代表溢出已经发生。

程序3-4  避免溢出的技巧

 

现在让我们轻松一下吧。设想一下如果一个程序员生了四个女儿，你如何给她们起名字呢？大女儿就叫“玲玲”吧，二女儿叫“玲依”，三女儿叫“依玲”，那么四女儿呢？你一定猜到了，按照这个顺序，就应该叫“依依”了。没错了，在软件学院我的学生里面，就有一个叫“张依依”的女生，不知道她是不是她爸爸的第四个女儿。让我们继续下去，如果这个程序员生下了第五个女儿，那么应该叫什么呢？按照上面介绍过的内容，她应该叫“忆初”了！希望你们能通过这些美丽的女孩名字记住上面讲到的内容，并衷心祝愿这个程序员早日生一个男孩。

3.4  无符号数

前面已经介绍了整数的二进制表示方法，对于n位二进制数，也就只能表示2ⁿ个整数。一个顺其自然的想法就是用这2ⁿ个整数的一半来表示正数，另外一半来表示负数。这种表示方法就是有符号数了。

但是在实际的应用中，有很多智榭鍪遣换岢鱿指菏摹１热缢滴颐堑哪炅洌桓霭嗉兜目纬淌桓龉业娜耸取Ｈ绻糜蟹攀幢４嬲庑┲担敲从涝恫换嵊玫奖硎靖菏哪且话敕段В庋捅话装桌朔蚜耍一故沟谜谋硎痉段П徽加昧艘话搿�

针对这个问题，C语言中引入了无符号数的概念。无符号数的源码、反码、补码都一致，具体的表示方法请参考3.1节中的介绍。对于n位二进制数，表示0到2ⁿ⁻¹ −1范围内的整数。

注意，无符号这个特性，只适用于整型数，而不适用于浮点数。同时我们一定要注意在表达式中混用有符号和无符号数的情况。这是因为C语言的表达式中会发生一种比较神奇的隐式数据类型转换，这种隐式的数据转换会带来一些隐含错误，如程序3-5中所示。

程序3-5　无符号整型数溢出实例

 

程序3-5中的Sum函数是一段非常中规中矩的程序，每个细节都考虑得很好。数组的长度length不可能是负的，所以声明为unsigned。在程序3-5第4行的表达式i<=length-1中，由于length是一个无符号整数，整个表达式length-1最后的结果也被隐式转换为无符号类型。这样，当length=0的时候，整个表达式变为了0U-1U，在3.3.2节中的图3-7中，下溢出正好对应这种情况。最后造成的结果就是，当length=0的时候，表达式length-1的值是最大的无符号数UINT_MAX，这样for循环就会执行UINT_MAX次。不过你不用担心，for循环不会真的执行UINT_MAX次，因为它会因为执行非法的内存访问而被操作系统一脚踢出。

与此类似的一个情况如程序3-5中的第9～11行所示，这段程序会打印出“???”。因为在表达式中会发生隐式类型转换，所以-1被转换成了无符号类型。别忘了，-1的二进制表示（全部二进制位都是1）在无符号整数中被定义为UINT_MAX。

无符号数据类型另外的一个主要隐含错误来源于sizeof，我们在3.9节会给出另外一个实例。本来无符号数是为了能扩大其表示的范围，但是却带来了很多的隐含错误，有点得不偿失了。所以，尽量不要在你的程序中使用无符号类型，以免增加不必要的复杂性，尤其不要仅仅因为无符号类型不存在负数而使用它来表示一个数值。随着计算机机器字长从32位过渡到64位，一个有符号数据类型int所表示的范围已经很大了，基本的问题都可以hold住，别忘了，实在不行还有long long类型。用int数据类型的好处在于，当涉及混合类型操作(比如比较有符号数和无符号数)的时候，我们不必担心上面描述的边界溢出情况(比如-1会被提升为一个非常大的正数)。我的一个建议就是：避免在一个表达式中混合使用无符号数和有符号数。

如果你一定要用，最好在表达式中使用强制类型转换，使它们同时为有符号数或无符号数，精确地告诉编译器你想干什么，别让编译器隐式地替你拿主意。

目前，无符号数多用在位段以及位操作上。在位操作中，有的时候需要逻辑移位，而不是数学移位，这个时候我们就必须用无符号数了。关于什么是逻辑移位，我们在4.7节中再详细讨论。

3.5  int和char的关系

3.5.1  char就是short short

整数类型有long，在本书发表的时期，大部分个人计算机都是32位的。在这样的计算机上，long的长度为32位，short是16位。如果你觉得位数比较少，你可以使用一个long long类型，这个类型是64位。其实，我们每一个人在初中英语中就已经接触过这个类型了，我们都非常熟悉的“long long ago”，就是声明了一个类型为long long数据类型的变量，变量名为ago，所以我说，所有的学问彼此都是相通的。如果C语言中有long long类型（64位），那么，有没有short short类型（8位）呢？答案是有，也没有！

为避免你们把鸡蛋扔过来，我必须尽快地揭晓这个答案。之所以说没有，就是因为如果你在代码中使用short short声明一个变量的时候，编译器会向你大声的咆哮：“error C2632，“short”后面的“short”非法”。之所以说有，那就是C语言中已经默认有一个short short类型（8位），那就是char。

千言万语赶紧汇成一句话，那就是，char就是一个8位整数。如果你还是纠结于char这个名字，就干脆把它想成short short吧！那char这个名字从何而来呢？其实这要拜ACSII码所赐。ACSII码规定用8位二进制数对256个字符进行编码。所以，这种8位二进制数的整型数据类型就叫作char了。从这个意义上说，程序3-6中前3行是正确而且合理的，就是看起来有点别扭罢了。我们可以把char赋值给一个int，这是安全的；反之，就要冒数据被截断而丢失的风险。毕竟要老鼠去住大象的房间是安全的，但是如果要把大象塞到冰箱里，却不太容易。

 

程序3-6　char与int互换

3.5.2  char的符号

如果short short类型存在，那么它一定是有符号的，除非你用unsigned来修饰它。但是char到底是有符号，还是无符号呢？答案是：有时候是有符号，有时候是无符号。你手中的鸡蛋最终还是飞了过来！我真的有点冤枉，事实就是如此。别忘耍�C语言有很多的编译器，每种编译器对char的符号都有自己的定义。任何先入为主的假设都是有风险的。

当要在不同平台移植我们的程序时，字符是否有符号的这种歧义性会给我们带来很大的麻烦。如果移植性的要求很高，那么你就需要确保你的字符变量中保存的值的范围在0到127之间，这样无论字符类型是否有符号，都可以正确地表示这个范围之内的值。

下面我们再来看一种提高移植性的方法，先查看一下函数getchar()的参考文档，官方的定义如下：int getchar()。有些同学可能会感到有点迷惑，getchar()明明返回一个字符，为什么要用一个int来接收呢。因为getchar()在读到文件末尾或者错误的时候，会返回EOF，EOF在stdio.h中被定义为-1[④]。如果你的平台上char恰巧是无符号的，程序3-7将永远不会停止。如果getchar()返回一个int型，同时我们在程序3-7中将第1行修改为int c;，这样，无论char是否有符号，程序3-7都可以通过判断c是否等于EOF来终    止了。

程序3-7　getchar的返回值

 

有没有一个办法确定，在我自己的计算机上，char到底是有符号的还是无符号的呢？还记得表3-1吗？其中有两个宏定义，分别为CHAR_MIN和CHAR_MAX。

猜到怎么做了吗？如果printf("%d",CHAR_MIN);输出的是-128，那么说明，在你的本地计算机上，char是有符号的；如果printf("%d",CHAR_MIN);输出的是0，那么说明，在你的本地计算机上，char是无符号的。

3.6  浮点数的有效位

整型数在计算机内部是用二进制的补码来表示的，那么浮点数呢？浮点数通常用一个分数和以某个基数的指数来组成，以m×b^e的方式保存在电脑中，一般电脑中基数b和分数m都是用二进制表示的。

例如，我们非常熟悉的PI=3.14159这个值是如何在计算机内部表示的呢？

它被表示成了.110010010000111111 × 2²的样子，也就是表示成

                                                                   

请注意，上面的表示方法只是一种候选方案，浮点数的具体表示方式并没有标准，这里涉及到一个取舍，相同的二进制位数，如果给m多分配些，浮点数的有效位就多些；如果给e多分些，浮点数表示的范围就大些。

鉴于浮点数的这种表示方法，它可以容纳更大范围内的数。例如，C语言中float所能表示的范围为10⁻³⁸到10³⁸，这已经是一个很大的范围了。虽然从理论上说，浮点数也存在溢出的问题，但是现实中，这并不是浮点数面临的主要问题。浮点数真正困扰我们的是它的精度，也就是它的有效位问题。我们运行程序3-8来说明。

程序3-8　浮点数的有效位

 

程序3-8会给出图3-9所示的结果，可以看出，无论是浮点数的运算，还是强制类型转换或者是利用scanf函数输入，由于浮点数的有效位问题，最终显示的浮点数都是不对的。因为通常float类型的有效位只为6位或7位，后面的数字都是编译器随机猜的了。

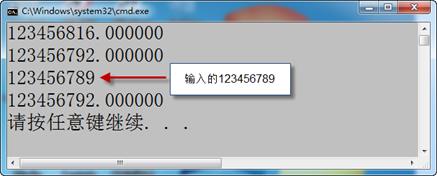
图3-9  程序运行结果

整型数的极限值都在limits.h头文件中定义。与此类似的是，无论是浮点数的表示范围，还是它的有效位，都在float.h头文件中定义。其中主要的宏定义如     表3-2所示。表中的各种宏定义都可以通过英文简单地猜测出来。

其中，表中FLT_MAX和FLT_MIN分别代表float所能保存的最大范围和最小范围。FLT_DIG代表的是float的有效位。FLT_MAX_EXP的官方英文含义是：“Maximum integer such that 10 raised to that number is a representable floating-point number”。不管你懂没懂，反正我是没懂。所以本书决定采用实例来进行说明，如果float所能保存的最大值为3.402823e+038，那么FLT_MAX_EXP就是上式中的那个38。

表3-2  浮点数的相关极限值

float	double	long double
FLT_MAX	DBL_MAX	LDBL_MAX
FLT_MIN	DBL_MIN	LDBL_MIN
FLT_DIG	DBL_MAX	LDBL_DIG
FLT_EPSILON	DBL_EPSILON	LDBL_EPSILON
FLT_MAX_EXP	DBL_MAX_EXP	LDBL_MAX_EXP
FLT_MIN_EXP	DBL_MIN_EXP	LDBL_MIN_EXP

 

程序3-9演示了这些宏定义的一些简单的用法。它的运行结果如图3-10所示。从结果可以看出，在我的电脑上，浮点数的有效位为6位，float所能保存的范围从1.175494e-038到3.402823e+038，这确实是一个很大的范围了。

程序3-9  浮点数的极限值定义

 

图3-10  程序运行结果

3.7  判断两个浮点数相等

如果你在表3-2中已经发现了FLT_EPSILON了，并且对这个东东产生了疑问，恭喜你！你很好学而且观察力出众。下面我来回答你的问题。像平常一样，我们的问题从程序3-10开始。整个程序如此简单，我想这里不用我进行进一步的解释了。

程序3-10  浮点数判断相等的错误方法

 

运行程序3-10后，在我的计算机上，即使我望穿秋水，也根本看不到控制台窗口上输出“Equal”。这是由浮点数的表示方法决定的。浮点数的具体表示方法我们在3.6节已经介绍过了，与整型数不同，浮点数的有效位只有6位或7位，所以浮点数保存的都是一个近似值。

两个近似值直接比较相等是不对的。为了解决这个问题，我们可以认为，如果两个近似值的差“足够小”，那么我们就认为这两个浮点数是相等的。而FLT_EPSILON就是定义这个“足够小”的。所以正确的比较方法见程序3-11中第2行。

程序3-11  浮点数判断相等的正确方法

 

判断两个浮点数是否相等，是一个很大的命题。例如100000.0与100001.0这两个浮点数，可以认为近似相等了，但是用程序3-11的方法却无能为力。关于判断浮点数相等的更多办法，读者可以参考本书网站上“扩展内容”网页中的“浮点数比较相等”。

3.8  常量与常量后缀

C语言中也可以直接包含数字常量，你可以用十进制、十六进制、八进制来定义他们。例如010表示的是八进制数，0x10表示的是十六进制数。这里注意一下，这两个数和10的值是不一样的，第一个表示十进制的8，第二个表示十进制的16。十六进制表示的数一般用于位运算，或者直接操作地址或硬件。

浮点型常量没有进制的区别，但是可以用两种方式表示，分别为小数形式和指数形式，如1.23或者1e10。对于整型常量，一般编译器默认其为int；对于浮点型常量，一般编译器默认为double类型。

为了用户能够准确地定义常量的类型，C语言用常量后缀的方式来指定常量的数据类型。如10UL表示这是一个unsigned long类型，1.2f表示这是一个浮点类型。下面给出一个稍微变态点的，那就是0xFUL，这个类似于UFO不明飞行物的东东也是一个整型常量，它用十六进制表示15，并且类型为unsigned long。

当我刚刚学习C语言的时候，我对这种后缀表示充满了疑问，10和10UL的真实值都是10，那么他们到底有什么区别？到目前为止，我都没有找到一个令我满意的答案。至少本书后面所列的所有参考书籍中都没有对常量后缀的用处给出详细的描述，所以我个人感觉这个东西可能没什么大用。如果你找到了常量后缀的杀手级应用，麻烦你告诉我一声。

没什么大用并不说明完全没有用。例如，有些函数有一个无符号型数据形参，这个时候，传入10UL要比传入10有更好的可读性和移植性。另外，表达式365*24*60*60在16位的电脑上会发生溢出，如果写成365*24*60*60UL，整个表达式就会被隐式转换成一个unsigned long类型，这样就不会发生溢出了。归根到底，常量后缀就是明确地告诉编译器：“请把我当成这种数据类型”，这样可以避免编译器的默认处理带来潜在的溢出或移植问题。

3.9  sizeof运算符

3.9.1  sizeof返回值

sizeof是C语言的一个关键字，不是一个函数。但是它的行为类似于一个函数，因为它返回一个类型为size_t的无符号的整型数。

size_t其实就是一个无符号的整型数。这一点很好理解，任何一个类型的size都不应该是负数。但就是这种无符号性，有的时候会给我们带来麻烦，如程序3-12所示。这段程序会打印出“str2 is longer than str1”，原因就在于我们前面介绍过的—溢出。这里我们最好复习一下前面讲过的溢出的知识。对于无符号数减法，必须要保证被减数大于减数，否则就会下界溢出而得到一个比较大的正数。这里正确的比较方法应该是if(strlen(str2)>strlen(str1))。

程序3-12　sizeof的返回值

 

3.9.2  sizeof的用处

考虑到字节对齐，C语言中struct的长度并不等于其中每个单个成员数据类型长度的和。其实不光是struct，我们对任何数据类型的长度的假设都不一定是正确的。这一点在我们利用二进制来读写文件的时候，就变得非常重要。所以当我们使用二进制来读写文件的时候，我们通常用sizeof来计算变量所占内存的真实尺寸，如程序3-13第5行所示。

程序3-13　sizeof的用法

 

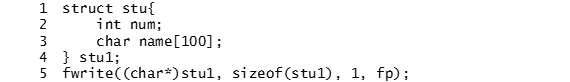
在不同的平台上，struct stu的尺寸都会被sizeof自动计算出来，所以程序3-13具有非常好的跨平台移植能力。

3.9.3  sizeof（指针）和sizeof（数组）的区别

学过C语言的都知道，指针和数组名代表的都是地址，有的地方可以互换，如程序3-14所示。

程序3-14  数组和指针关系

 

但是对sizeof，二者还是有区别的，如程序3-15所示。

程序3-15  数组和指针在sizeof上的区别

 

结果如图3-11所示。

图3-11  程序运行结果

从结果我们可以看出，对指针利用sizeof得到的都是一个相同的值。在C语言中，指针只保存一个地址，所以任何类型的指针都占用相同的字节数。对数组名利用sizeof得到的是整个数组占用的字节数。从程序3-15的第8行，我们可以学到一个技巧，那就是如何根据数组名a来计算数组到底有多少个元素。

3.10  本章小结

本章首先介绍了整型数的补码表示，在此基础上介绍了整型数的溢出问题。针对于浮点数，介绍了浮点数的有效位问题。为了方便大家记忆，我发明了一个口诀。正确的口诀不仅能打开充满宝藏的山洞，在现实生活中的作用也非常大。我在生活中往往非常粗心，总是丢东拉西的。直到有一天我在杂志上看到了一句口诀，那就是：“伸手要钱”，“伸—”身份证，“手—”手机，“要—”钥匙，“钱—”钱包。所以每次出门前，我都默念这个口诀，从此再也没被锁在房间外头过。现在的一些成功人士，一般都有两个手机，所以你可以修改这个口诀为：“伸两手要钱”。

下面介绍我的口诀，那就是：“296两宏两头”。这里我解释一下这个口诀，“29”表示整型数的上限大约为2×10⁹；“6”表示浮点数的有效位为6位；“两宏”分别表示_MAX类型宏和FLT_EPSILON宏；“两头”分别表示float.h和limits.h头文件。如果你能掌握本节介绍的全部内容，并记住这个口诀，那么你可以避免常见的整型数溢出和浮点数有效位的问题。最后提醒一下，口诀的力量虽然大，但是内容千万别记错了，芝麻开门是可以的，黄豆、大麦、土豆统统不行！

对于无符号数，有两条建议，不要因为你的变量不会出现负值就用无符号数来定义，同时避免在一个表达式中混合使用无符号数和有符号数。

sizeof是一个有趣的C语言关键字，对于它你要知道两点，首先它会返回一个无符号数；其次，当它作用于指针和数组的时候有不同的含义。大多数情况下，sizeof多被用在文件的二进制读写方面。

如果你在计算机上利用C语言编程了一段时间，可能会有一个默认的认识，那就是int的长度是4字节，这个认识是不对的。一个更为准确的认识是int的长度可能与CPU的字长一样。请注意，这里我只是说可能。伴随着物联网的兴起，计算无处不在，联网无处不在。不远的将来，可能你家的冰箱里、垃圾桶里，都会有一个CPU，都会联网。有一天，你家的垃圾桶会给你发短信，对你说：“我空了”，冰箱说：“我满了”，这说明你的生活状态还不错。如果短信的内容反过来，那么你的生活状态就比较糟糕了。无论怎么说，垃圾桶里的CPU的字长和计算机里的CPU的字长我猜不太可能一样，而C语言又是一门应用广泛、兼顾高端与低端的语言，所以也应该是给垃圾桶编程的首选。这样，当你要使用数据类型的长度时，用sizeof可以保证你的程序具有最大可能的跨平台移植性。例如，对垃圾桶判断“满”或是“空”的程序，就可以不加修改地移植到马桶上。综上所述，不要对任何数据类型的长度做先入为主的假设。你唯一能确定的就是：

sizeof(char)<=sizeof(short)<=sizeof(int)<=sizeof(long)