2.2 Recursive

• First, the inline specification on a function is just a hint. The compiler can (and often does) completely ignore the presence or absence of an inline qualifier. With that said, a compiler can inline a recursive function, much as it can unroll an infinite loop. It simply has to place a limit on the level to which it will "unroll" the function.
• One recursive(Factorial), Two recursive call( Hanoti) (Tree), Multi Recursive(Permutation)
• result is single (FActorial), Result is many steps,(Hanoti) (Maze), Result is a set( permutation). you can see that 1) any recursive function should at least one input parameter, and this parameter should to be pass sub-problem. 2) for return value, it has two different kind, if result is single value, you should return a value, such as Factorial. If result is set(permutation) or many steps(in-order traversal of treeor Hanoi tree), you can declare your function as void. 3) Some functions need input another parameter, such as level information in the tree or position information in the permutation. 4) Base case can be understood differently, most of time base case is 0 or null, but for permutation, base case is i==n. most subproblem, i decrease, but for permutation, for each subproblem i increase.
  1. single result
     int Factorial(int n){ 
     if (n == 1) 
          return 1; 
      return n*Factorial(n-1); 
     }
  2. result is serial steps (Hanoti) DFS(Maze)
     FUNCTION MoveTower(disk, source, dest, spare): 
     IF disk == 0, THEN: 
         move disk from source to dest 
     ELSE: 
         MoveTower(disk - 1, source, spare, dest)   // Step 1 above 
         move disk from source to dest              // Step 2 above 
         MoveTower(disk - 1, spare, dest, source)   // Step 3 above 
     END IF

     Result is a set( permutation)

• permutation, It is also worth noting that when you make a recursive call, you advance down an individual branch of the tree, and an additional branch is added with every iteration of a ’for’ or ’while’ loop. One confusing thing about this problem is the second swap after the recursive call to permute. This can be interpreted as ’unswap,’ and is required because the char array is passed by reference, not by value, and every time you swap elements in the array the change is visible down stream.
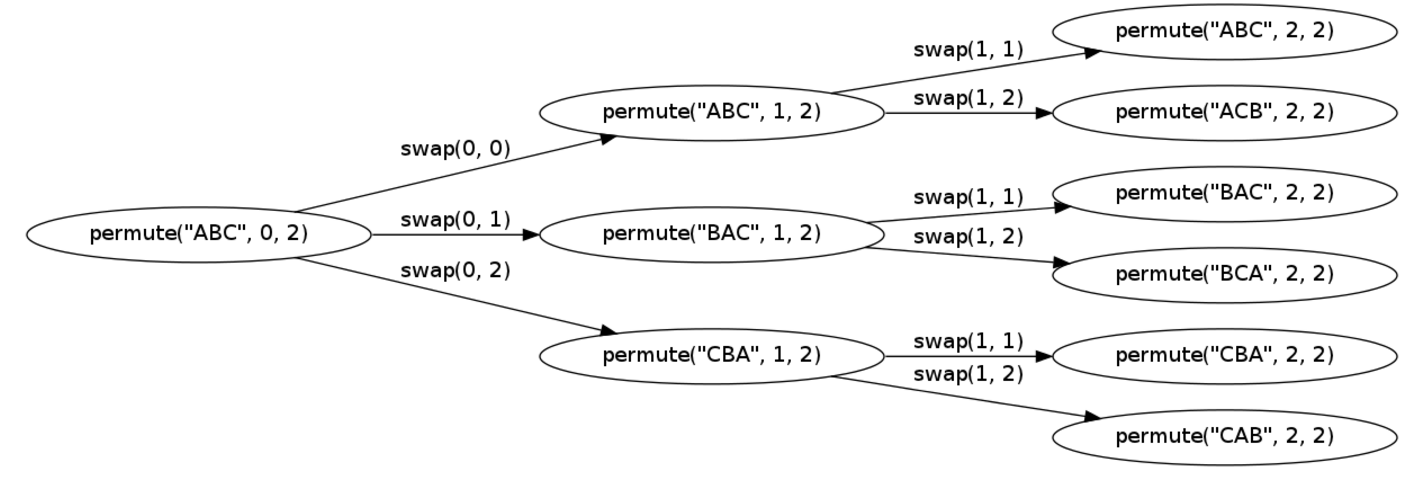
  void permute(char a[], int i, int n){ 
     int j; 
     if (i == n) 
       cout << a << endl; 
     else   { 
         for (j = i; j <= n; j++)       { 
            swap(a[i], a[j]); 
            permute(a, i+1, n); 
            swap(a[i], a[j]); 
         } 
     } 
  }

  

• It includes direct recursive and indirect recursive. direct recursive is R() call R() again in it’s funciton body. It has two parts: 1)base and 2) recursive component